The Foucault pendulum at the Department of Physics
by Franco Laeri
To claim that the earth rotates was life-threatening in the 1600s. We know what happened to some who did so anyway. It was therefore all the more important to present the most graphic evidence possible. Vincenzo Viviani (5.4.1622–22.9.1703) worked with Galileo Galilei in Florence and demonstrated such a proof in 1661 with the pendulum experiment, which became known 190 years later as Foucault's pendulum [1].
The pendulum shown at the Department of Physics corresponds in its dimensions approximately to the pendulum which Jean Bernard Léon Foucault (18.9.1819–11.2.1868) set up in the cellar of his mother's house in Paris, Rue d'Assas, on 03 January 1851 [2]. But more convincing was the 11-meter pendulum, which he installed after the invitation of François Arago in the Observatoire de Paris and a little later after the request of Louis Napoléon Bonaparte on March 26, 1851 under the dome in the Panthéon. The 67 m long pendulum can still be seen there today.
A few years later, Foucault constructed another pendulum for the 1855 World's Fair in Paris. In the Musée des Arts et Métiers in Paris, this pendulum has been on display since 1890 in the choir of the former church of Saint-Martin-des-Champs.
The pendulum masses of the pendulums are replicas of the original pendulums. The originals were bequeathed by Foucault to the Conservatoire des Arts et Métiers in Paris and are kept there.
Even after a shorter, more detailed observation of the pendulum, it becomes visible that the oscillation plane of the pendulum slowly turns clockwise. Now one would assume that the oscillation plane of the pendulum turns 360° in one day. But this is not the case. The observation shows that the pendulum has made a complete turn only after approx. 31 h. The plane of oscillation of the pendulum follows the plane of rotation of the pendulum. Thus, the plane of oscillation turns only 275° in one day. The observation also shows that this rotation depends on the geographical latitude of the place where the pendulum is set up. To what extent can this rotation be considered as a proof for the earth rotation? So let's try a description of the phenomenon. We want to neglect the effects of the air and other frictions and assume that the earth has a spherically symmetrical structure [3].
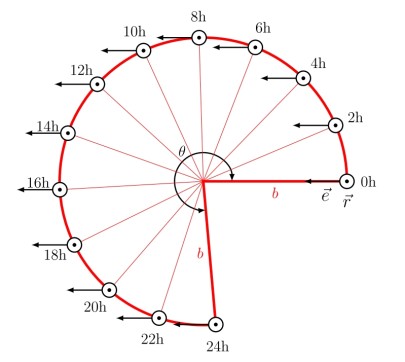
Geometry of the relevant vectors: unit vector e in the direction of the pendulum swing. Shown is the time t = 0 h at which the oscillation occurs exactly along the Darmstadt meridian.
Unit vector r in direction of the surface normal at the pendulum location Mathildenhöhe (geogr. latitude ϕ = 49.87° North). The tangent to the meridian sweeps over the cone surface drawn in red in the course of one revolution of the earth. The distance of the place DA (Darmstadt) to the cone apex is b. A simple geometrical consideration shows that the half opening angle of this cone is ϕ. Thus a = b sin ϕ results.
We describe the oscillation of the pendulum by the unit vector in the direction of the oscillation around the local normal at the latitude ϕ. Unit vector and normal span the instantaneous plane of oscillation of the pendulum. The pendulum mass is subjected to the gravitational force of the Earth, which is described by the gravitational acceleration g acting at the pendulum location.
If we approximate the structure of the earth [3] by assuming spherical symmetry, the normal ris parallel to the gravitational acceleration. However, the suspension point of the pendulum rotates with the earth, which would cause the pendulum to perform a precession motion. Especially for short pendulums (10 m and shorter), this precessional motion would be more pronounced than the Foucault rotation of the plane of oscillation. The precession motion is therefore artificially damped in these cases by special measures.
One method which has proved very successful was realized by Fernand Charron in the form of a small ring under the suspension point [4]. With the “Charron ring” it is possible to realize a “precision-free” pendulum. We want to assume such a pendulum for the further consideration. Therefore, we now assume that apart from the gravitational force, no other forces act on the pendulum. Under these conditions (Charron ring) and because the gravitational force is constant in time, the pendulum does not perform any rotation around the normal.
In the figure above, the geometry is shown at a time t = 0 h, when the oscillation is just in the direction of the meridian. If we consider the tangent to the meridian, this tangent sweeps over a cone, the tangent cone to the latitude circle of the installation site, in the course of a day. The pendulum does not change its direction of oscillation during this time under said conditions, i.e. the unit vector of the direction of the oscillation always points in the same direction in the space of the fixed stars, since no force acts except the gravitational force (spherically symmetrical force field). However, an observer who observes the pendulum notes that in his reference frame, which is characterized by its geografical coordinates, the plane of oscillation rotates slowly. After one sidereal day, the meridian b is again in its initial position.
Now, after one rotation of the earth, how is the direction of oscillation oriented for an observer on earth?
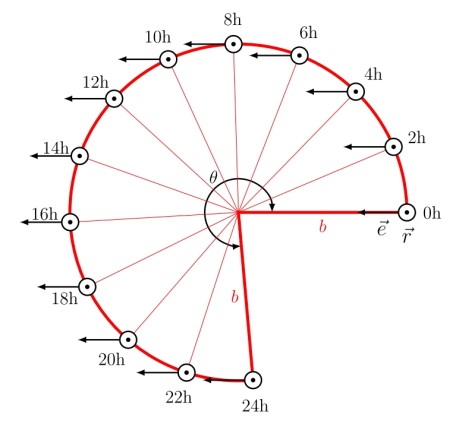
For a better understanding of the geometry, the red cone surface of the above figure is drawn here in the development. The red circumference line corresponds in this representation to the latitude circle of Darmstadt (geogr. latitude ϕ = 49, 87° north).
The surface line b (i.e. tangent to the Darmstadt meridian) turns around the center of the circle in one day and sweeps the whole cone (red dashed line).
At the time 0 h the pendulum swings in direction e(0 h), which at this time shows just parallel to the local meridian. The normal r at the place Darmstadt stands in this representation at each time perpendicularly on the plane of the unwinding. A person standing on the earth (his reference are meridian and parallel circle) sees how in the course of time t the pendulum swing slowly changes direction. After one day (exactly taken one 'star day' = 23,9345 h) r(24 h) and the tangent to the meridian b in the space of the fixed stars point again in the original direction. The direction of oscillation of the pendulum e(24 h), on the other hand, now takes the angle θ with respect to the local meridian.
Shown are the angular ratios corresponding to the geographical position of Darmstadt. Accordingly, after one sidereal day, the plane of oscillation has not made a complete turn, but only θ = 275°.
Which movement the pendulum has carried out can be described most vividly in the unwinding of the cone surface, which the meridian b sweeps over in the course of the day. In this representation every 2 hours a snapshot of the surface normal, which is perpendicular to the drawing plane here, and of the oscillation vector, which lies in the drawing plane, are shown (e lies perpendicular to r).
The pendulum shifts in the course of the earth rotation along the red circle. Thus the angle, which arises in the course of the time between the meridian and the oscillation plane, can be read off here simply. If the pendulum swings at the time t = 0 in the direction of the meridian – i.e. parallel to b – one finds that the direction of oscillation moves away from the meridian in the course of time. After 24 h (to be precise, one 'sidereal day' = 23.9345 h) – that is, one rotation of the Earth – the direction of oscillation of the pendulum has rotated by the angle θ.
From the geometry of the situation, the radius of the circle of latitude gives a = b sin ϕ:
θ = 360° × sin ϕ = 275°.
Quintessence: The Foucault pendulum explicitly proves the earth's rotation.
Note 1: In practical realization, the pendulum is never free from external influences, such as draught or bearing friction. Therefore, the observed rotation of the plane of oscillation will differ from the calculated rotation [5].
Note 2: The rotation of the plane of oscillation is traditionally described by the action of an “apparent force”, the Coriolis force [6]. However, the fact that the rotation of the oscillation plane of the Foucault pendulum is independent of dynamically effective parameters, such as pendulum mass or pendulum length, but is determined solely by geographical quantities, is an indication of the geometric nature of this effect and thus of the Coriolis force. In a more general context, the Effect can also be understood as the parallel transport of the local, two-dimensional velocity field of the pendulum along a closed but noninertial space curve. Such questions about motion in curved spaces are especially central in general relativity. However, in optics or wave mechanics, analogous phenomena are also known as “geometric phase” [7] or “Berry phase” [8].
Note 3: In principle, no motion can be defined without a reference frame. Therefore, the question arises in which frame of reference the motion of the Foucault pendulum, i.e., the orientation of its plane of oscillation, should be considered. At the time of Foucault, this was not a particularly controversial question, because the existence of an absolute space according to Newton was almost universally agreed upon. Then, at the end of the 19th century, Ernst Mach was among the critics of this idea. He postulated that the motion of a body can be meaningfully determined only in relation to other bodies (he thought of fixed stars). Accordingly, in an empty universe, space would not be observable, and the orientation of the swing of a pendulum would be meaningless. The observation of the pendulum by Foucault clearly shows that the plane of its oscillation is stationary aligned in the space of the fixed stars. The space of the fixed stars (astronomers today would speak of the local group) would therefore be the natural reference frame for the description of the pendulum. Einstein, however, does not presuppose a preferred reference frame in the special theory of relativity.
General relativity, on the other hand, implies a space-time structure with a real physical experience. The Foucaultexperiment should therefore also be considered in this framework. Thereby, the pendulum would be subject to a general relativistic perturbation, the Lense-Thirring-Effect, which could be proven experimentally. The Lense-Thirring-Effect states that the rotation of the earth's mass slightly twists Einstein's space-time. If the pendulum would be anchored in the general-relativistic space-time, deviations in the rotation of the oscillation plane would have to result consequently opposite an anchoring in the Machian fixed star system. However, the Effect is too small to be proven with today's measuring methods. Whether there really is a preferred reference frame therefore remains a question to speculate about.
There are quite a few experiments underway on the Lense-Thirring Effect; cf. [9]. The Lense-Thirring-Effect could also be responsible for the strong plasma jets at black holes, which leads to very energetic cosmic rays whose particles have been registered on Earth with energies up to 1021 eV.
Acknowledgments: The author thanks Pia Domschke for Tikz programming of the figures and Reinhold Walser for critical review and additions to the text.