Das Pendel von Foucault am Fachbereich Physik
von Franco Laeri
Zu behaupten, dass die Erde sich drehe, war um 1600 lebensgefährlich. Wie es einigen ergangen ist, die dies trotzdem taten, wissen wir. Umso wichtiger war es daher, dafür möglichst anschauliche Beweise vorzulegen. Vincenzo Viviani (5.4.1622-22.9.1703) hat mit Galileo Galilei in Florenz gearbeitet und mit dem Pendelversuch, der 190 Jahre später als Pendel von Foucault bekannt wurde, 1661 einen solchen Beweis demonstriert [1].
Das am Fachbereich Physik gezeigte Pendel entspricht in seinen Maßen etwa dem Pendel, das Jean Bernard Léon Foucault (18.9.1819-11.2.1868) am 03. Januar 1851 im Keller des Hauses seiner Mutter in Paris, Rue d'Assas, aufstellte [2]. Überzeugender war aber das 11-Meter-Pendel, das er nach der Einladung von François Arago im Observatoire de Paris und wenig später nach der Aufforderung von Louis Napoléon Bonaparte am 26. März 1851 unter der Kuppel im Panthéon installiert wurde. Das 67 m lange Pendel ist da noch heute zu sehen.
Einige Jahre später konstruierte Foucault für die Weltausstellung 1855 in Paris ein weiteres Pendel. Im Musée des Arts et Métiers in Paris ist diese Pendel seit 1890 im Chor der ehemaligen Kirche von Saint-Martin-des-Champs zu besichtigen.
Die Pendelmassen der Pendel sind Replikas der originalen Pendel. Die Originale wurden von Foucault dem Conservatoire des Arts et Métiers in Paris vermacht und sind dort aufbewahrt.
Schon nach einer kürzeren, genaueren Beobachtung des Pendels wird sichtbar, dass die Schwingungsebene des Pendels sich langsam im Uhrzeigersinn dreht. Nun würde man annehmen, dass sich die Schwingungsebene des Pendels in einem Tag um 360° dreht. Dem ist aber nicht so. Die Beobachtung ergibt, dass das Pendel erst nach ca. 31 h eine ganze Drehung vollzogen hat. Die Schwingungsebene dreht sich demnach in einem Tag lediglich um 275°. Aus der Beobachtung ergibt sich auch, dass diese Drehung von der geographischen Breite des Aufstellungsortes des Pendels abhängt. Inwiefern kann diese Drehung als Beweis für die Erdrotation gelten? Versuchen wir also eine Beschreibung des Phänomens. Dabei wollen wir die Effekte der Luft- und anderen Reibungen vernachlässigen und annehmen, die Erde hätte einen kugelsymmetrischen Aufbau [3].
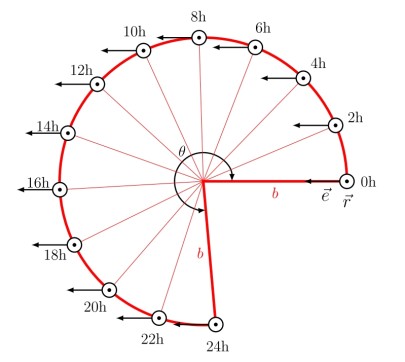
Geometrie der relevanten Vektoren: Einheitsvektor e in Richtung der Pendelschwingung. Dargestellt ist der Zeitpunkt t = 0 h, zu dem die Schwingung genau entlang des Darmstadt-Meridians erfolgt.
Einheitsvektor r in Richtung der Oberflächennormale am Pendelort Mathildenhöhe (geogr. Breite ϕ = 49,87° Nord). Die Tangente an den Meridian überstreicht im Laufe einer Erdumdrehung die rot gezeichnete Kegelfläche. Der Abstand des Ortes DA (Darmstadt) zur Kegelspitze betrage b. Eine einfache geometrische Überlegung ergibt, dass der halbe Öffnungswinkel dieses Kegels ϕ beträgt. Damit ergibt sich a = b sin ϕ.
Die Schwingung des Pendels beschreiben wir durch den Einheitsvektor in Richtung der Schwingung um die lokale Normale bei der geographischen Breite ϕ. Einheitsvektor und Normale spannen die momentane Schwingungsebene des Pendels auf. Die Pendelmasse ist der Gravitationskraft der Erde ausgesetzt, die durch die am Pendelort wirkende Gravitationsbeschleunigung g beschrieben wird.
Nähern wir den Aufbau der Erde [3] indem wir Kugelsymmetrie annehmen, so ist die Normale rparallel zur Gravitationsbeschleunigung. Der Aufhängepunkt des Pendels jedoch dreht sich mit der Erde, was dazu führen würde, dass das Pendel eine Präzessionsbewegung ausführt. Besonders bei kurzen Pendeln (10 m und kürzer) wäre diese Präzessionsbewegung stärker ausgeprägt als die Foucault-Drehung der Schwingungsebene. Die Präzessionsbewegung wird deshalb in diesen Fällen durch spezielle Massnahmen künstlich gedämpft.
Eine Methode, die sich sehr bewährt hat, hat Fernand Charron in Form eines kleinen Rings unter dem Aufhängungspunkt realisiert [4]. Mit dem „Charron-Ring“ gelingt es, ein „präzessionsfreies“ Pendel zu realisieren. Ein solches wollen wir für die weitere Betrachtung voraussetzen. Daher nehmen wir nun an, dass außer der Gravitationskraft keine weiteren Kräfte auf das Pendel wirken. Unter diesen Voraussetzungen (Charron-Ring) und weil die Gravitationskraft zeitlich konstant ist, führt das Pendel keine Rotation um die Normale durch.
In der obigen Abbildung ist die Geometrie zu einem Zeitpunkt t = 0 h dargestellt, zu dem die Schwingung gerade in Richtung des Meridians erfolgt. Betrachtet man die Tangente an den Meridian, so überstreicht diese Tangente im Laufe eines Tages einen Kegel, den Tangentialkegel an den Breitenkreis des Aufstellungsorts. Das Pendel ändert während dieser Zeit unter besagten Bedingungen seine Schwingungsrichtung nicht, d. h. der Einheitsvektor der Richtung der Schwingung zeigt im Raum der Fixsterne immer in die gleiche Richtung, da ja außer der Gravitationskraft keine Kraft wirkt (kugelsymmetrisches Kraftfeld). Ein Betrachter, der das Pendel beobachtet, stellt aber fest, dass sich in seinem Bezugssystem, das durch seine geografischen Koordinaten charakterisiert sei, die Schwingungsebene langsam dreht. Nach einem Sterntag liegt der Meridian b wieder in seiner Ausgangslage.
Wie ist nun jetzt, nach einer Erdumdrehung, die Schwingungsrichtung für einen Betrachter auf der Erde orientiert?
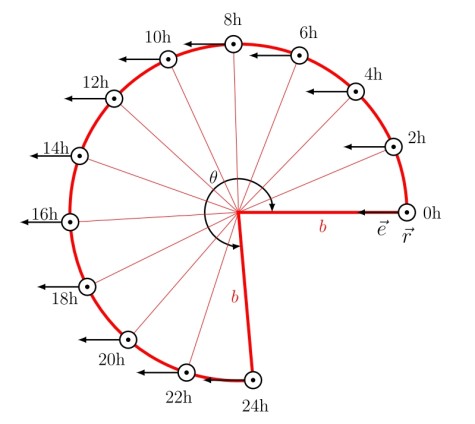
Zum besseren Verständnis der Geometrie ist die rote Kegelfläche der obigen Abbildung hier in der Abwicklung gezeichnet. Die rote Umfangslinie entspricht in dieser Darstellung dem Breitenkreis Darmstadts (geogr. Breite ϕ = 49, 87° Nord).
Die Mantellinie b (d. h. Tangente an den Darmstadt-Meridian) dreht sich in einem Tag um das Kreiszentrum und überstreicht dabei den ganzen Kegel (rot gestrichelt).
Zum Zeitpunkt 0 h schwinge das Pendel in Richtung e(0 h), die zu diesem Zeitpunkt gerade parallel zum lokalen Meridian zeigt. Die Normale r am Ort Darmstadt steht in dieser Darstellung zu jedem Zeitpunkt senkrecht auf der Ebene der Abwicklung. Ein auf der Erde stehender Mensch (sein Bezug sind Meridian und Breitenkreis) sieht, wie im Laufe der Zeit t die Pendelschwingung langsam die Richtung ändert. Nach einem Tag (genau genommen einem ‚Sterntag‘ = 23,9345 h) zeigen r(24 h) und die Tangente an den Meridian b im Raum der Fixsterne wieder in die ursprüngliche Richtung. Die Schwingungsrichtung des Pendels e(24 h) hingegen, nimmt nun gegenüber dem lokalen Meridian den Winkel θ ein.
Dargestellt sind die Winkelverhältnisse, die der geographischen Lage Darmstadts entsprechen. Nach einem Sterntag hat demnach die Schwingungsebene nicht eine ganze Drehung durchgeführt, sondern nur θ = 275°.
Welche Bewegung das Pendel durchgeführt hat, lässt sich am anschaulichsten in der Abwicklung der Kegelfläche beschreiben, die der Meridian b im Laufe des Tages überstreicht. In dieser Darstellung sind alle 2 Stunden eine Momentaufnahme der Flächennormalen, die hier senkrecht zur Zeichenebene steht und des Schwingungsvektors, der in der Zeichenebene liegt, dargestellt (e liegt ja senkrecht zu r).
Das Pendel verschiebt sich im Laufe der Erddrehung entlang des roten Kreises. Somit lässt sich hier der Winkel, der sich im Laufe der Zeit zwischen dem Meridian und der Schwingungsebene ergibt, einfach ablesen. Schwingt das Pendel zum Zeitpunkt t = 0 in Richtung des Meridians – also parallel zu b – so stellt man fest, dass sich die Schwingungsrichtung im Laufe der Zeit vom Meridian entfernt. Nach 24 h (genau genommen einem ‚Sterntag‘ = 23,9345 h) – also einer Erddrehung – hat sich die Schwingungsrichtung des Pendels um den Winkel θ gedreht.
Aus der Geometrie der Situation ergibt sich mit dem Radius des Breitenkreises a = b sin ϕ:
θ = 360° × sin ϕ = 275°
Quintessenz: Das Foucaultpendel weist die Erddrehung explizit nach.
Bem. 1: In der praktischen Realisierung ist das Pendel nie frei von äußeren Einflüssen, wie Zugluft oder Lagerreibung. Daher wird die beobachtete Drehung der Schwingungsebene von der berechneten Drehung abweichen [5].
Bem. 2: Die Drehung der Schwingungsebene wird traditionell durch das Wirken einer „Scheinkraft“, der Corioliskraft, beschrieben [6]. Dass die Drehung der Schwingungsebene des Foucaultpendels aber von dynamisch wirksamen Parametern, wie Pendelmasse oder Pendellänge unabhängig ist, sondern allein durch geographische Größen bestimmt wird, ist ein Hinweis auf die geometrische Natur dieses Effekts und damit der Corioliskraft. In einem allgemeineren Zusammenhang kann man den Effekt auch als Paralleltransport des lokalen, zweidimensionalen Geschwindigkeitsfeldes des Pendels entlang einer geschlossenen, aber nichtinertialen Raumkurve verstehen. Solche Fragen nach der Bewegung in gekrümmten Räumen sind besonders in der Allgemeinen Relativitätstheorie von zentraler Bedeutung. In der Optik oder Wellenmechanik kennt man aber auch analoge Phänomene als „geometrische Phase“ [7] oder „Berry-Phase“ [8].
Bem. 3: Grundsätzlich kann ohne ein Bezugssystem keine Bewegung definiert werden. Es stellt sich daher die Frage, in welchem Bezugssystem die Bewegung des Foucault-Pendels, d. h. die Orientierung seiner Schwingungsebene, zu betrachten ist. Zur Zeit Foucaults war dies keine besonders umstrittene Frage, denn die Existenz eines absoluten Raumes gemäß Newton fand fast überall Zustimmung. Dann, Ende des 19. Jh., gehörte Ernst Mach zu den Kritikern dieser Idee. Er postulierte, dass die Bewegung eines Körpers allein im Bezug zu anderen Körpern (er dachte an Fixsterne) sinnvoll bestimmbar ist. In einem leeren Universum wäre demnach der Raum nicht beobachtbar, und die Ausrichtung der Schwingung eines Pendels wäre sinnfrei. Die Beobachtung des Pendels von Foucault ergibt eindeutig, dass die Ebene seiner Schwingung im Raum der Fixsterne stationär ausgerichtet ist. Der Raum der Fixsterne (Astronomen heute würden von der lokalen Gruppe sprechen) wäre demnach das für die Beschreibung des Pendels natürliche Bezugssystem. Einstein setzt in der Speziellen Relativitätstheorie jedoch kein bevorzugtes Bezugssystem voraus.
Die Allgemeine Relativitätstheorie hingegen impliziert eine Raum-Zeit-Struktur mit einer reellen physikalischen Erfahrbarkeit. Das Foucaultexperiment sollte daher auch in diesem Rahmen betrachtet werden. Dabei wäre das Pendel einer allgemein-relativistischen Störung unterworfen, dem Lense-Thirring-Effekt, der sich experimentell nachweisen ließe. Der Lense-Thirring-Effekt besagt, dass die Rotation der Erdmasse die Einsteinsche Raum-Zeit leicht verdreht. Wenn das Pendel in der allgemein-relativistischen Raum-Zeit verankert wäre, müssten sich demzufolge gegenüber einer Verankerung im Machschen Fixsternsystem Abweichungen in der Drehung der Schwingungsebene ergeben. Der Effekt ist jedoch zu klein, um mit heutigen Messmethoden nachgewiesen werden zu können. Ob es wirklich ein bevorzugtes Bezugssystem gibt, bleibt deshalb eine Frage, über die spekuliert werden kann.
Zum Lense-Thirring-Effekt sind etliche Experimente am laufen; vgl. [9]. Der Lense-Thirring-Effekt könnte auch für die starken Plasmajets bei schwarzen Löchern verantwortlich sein, die zu sehr energiereicher kosmischer Strahlung führt, deren Partikel auf der Erde mit Energien bis 1021 eV registriert wurden.
Danksagung: Der Autor dankt Pia Domschke für die Tikz-Programmierung der Figuren und Reinhold Walser für die kritische Durchsicht und Ergänzungen des Textes.